|
|
@@ -140,12 +140,49 @@ The coding algorithm works with probabilities for symbols in an alphabet. From a
|
|
|
R_{i} = R_{i-1} \cdot p_{j}
|
|
|
\end{equation}
|
|
|
}
|
|
|
+% math and computers
|
|
|
+Bevore getting into the arithmetic coding algorithm, the following section will go over some details on how digital fractions are handled by computers. This knowledge will be helpfull in understanding how arithmetic coding works.\\
|
|
|
+In computers, arithmetic operations on floating point numbers are processed with integer representations of given floating point number \cite{ieee-float}. The number 0.4 + would be represented by $4\cdot 10^{-1}$.\\
|
|
|
+A interval would be represented by natural numbers between 0 and 100 and $... \cdot 10^-x$. \texttt{x} starts with the value 2 and grows as the intgers grow in length, meaning only if a uneven number is divided. For example: Dividing a uneven number like $5\cdot 10^{-1}$ by two, will result in $25\cdot 10^{-2}$. On the other hand, subdividing $4\cdot 10^y$ by two, with any negativ real number as y would not result in a greater \texttt{x} the length required to display the result will match the length required to display the input number \cite{witten87, moffat_arith}.\\
|
|
|
+Binary fractions are limited in from of representing decimal fractions. This is due to the fact that every other digit, adds zero or half of the value before. In other terms: $b \cdot 2^{-n}$ determines the value of $b \in {0,1}$ at position n behind the decimal point.\\
|
|
|
+
|
|
|
+
|
|
|
+%todo example including figure
|
|
|
+% example unscaled
|
|
|
+\begin{figure}[H]
|
|
|
+ \centering
|
|
|
+ \includegraphics[width=15cm]{k4/arith-unscaled.png}
|
|
|
+ \caption{Illustrative example of arithmetic coding.}
|
|
|
+ \label{k4:arith-unscaled}
|
|
|
+\end{figure}
|
|
|
+
|
|
|
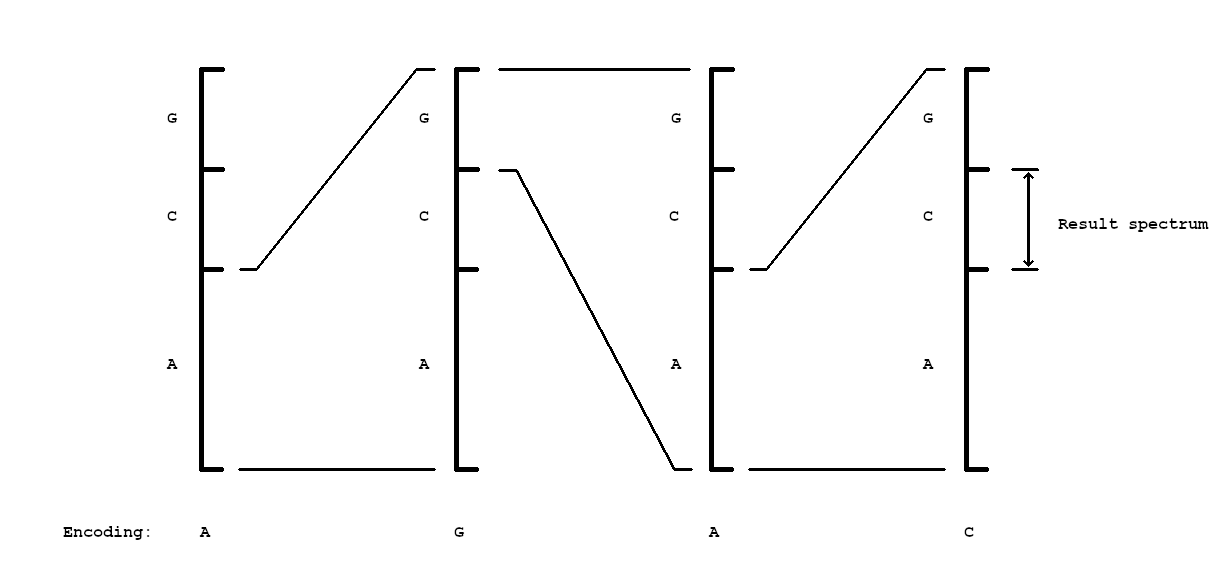
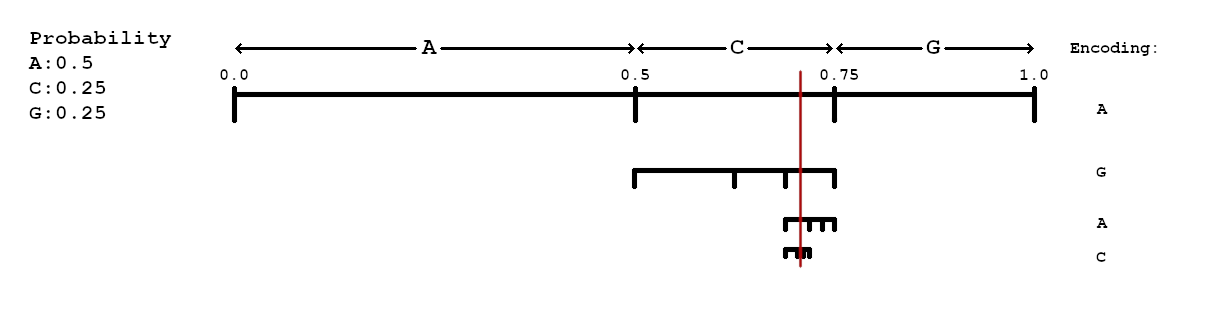
+The encoding of the input text, or a sequence is possible by projecting it on a binary encoded fraction between 0 and 1. To get there, each character in the alphabet is represented by an interval between two fractions, in the space between 0.0 and 1.0. In \ref{k4:arith-unscaled} this space is illustraded by the line in the upper center, with a scaling form 0.0 on the left, to 1.0 on the right side. The interval for each symbol is determined by its distribution, in the input text (interval start) and the the start of the next character (interval end). The sum of all intervals will result in one \cite{moffat_arith}.\\
|
|
|
+In order, to remain in a presentable range, the example in \ref{k4:arith-unscaled} uses an alphabet of only three characters: \texttt{A, C and G}. For the sequence \texttt{AGAC} a probability distribution as shown in the upper left corner and listed in \ref{t:arith-prob} was calculated. The intervals resulting from this probabilities, are visualized by the three sections marked by outwards pointing arrows at the top. The interval for \texttt{A} extends from 0.0 until the start of \texttt{C} at 0.5, which extends to the start of \texttt{G} at 0.75 and so on.\\
|
|
|
|
|
|
-%todo ~figures~
|
|
|
+\label{t:arith-prob}
|
|
|
+\sffamily
|
|
|
+\begin{footnotesize}
|
|
|
+ \begin{longtable}[c]{ p{.2\textwidth} p{.2\textwidth} p{.5\textwidth}}
|
|
|
+ \caption[Probability distribution for arithmetic encoding example shown in \ref{k4:arith-unscaled}] % Caption für das Tabellenverzeichnis
|
|
|
+ {Probabilities for \texttt{A,C and G} as shown in example \ref{k4:arith-unscaled}} % Caption für die Tabelle selbst
|
|
|
+ \\
|
|
|
+ \toprule
|
|
|
+ \textbf{Symbol} & \textbf{Probability} & \textbf{Interval}\\
|
|
|
+ \midrule
|
|
|
+ A & $\frac{2}{4}=0.11$ & ${x\in \mathbb{Q} | 0.0 <= x < 0.5}$\\
|
|
|
+ C & $\frac{1}{4}=0.71$ & ${x\in \mathbb{Q} | 0.5 <= x < 0.75}$\\
|
|
|
+ G & $\frac{1}{4}=0.13$ & ${x\in \mathbb{Q} | 0.75 <= x < 1.0}$\\
|
|
|
+ \bottomrule
|
|
|
+ \end{longtable}
|
|
|
+\end{footnotesize}
|
|
|
+\rmfamily
|
|
|
|
|
|
-This is possible by projecting the input text on a binary encoded fraction between 0 and 1. To get there, each character in the alphabet is represented by an interval between two floating point numbers in the space between 0.0 and 1.0 (exclusively). This interval is determined by the symbols distribution in the input text (interval start) and the the start of the next character (interval end). The sum of all intervals will result in one \cite{moffat_arith}.\\
|
|
|
-To encode a text, subdividing is used, step by step on the text symbols from start to the end. The interval that represents the current character will be subdivided. Meaning the choosen interval will be divided into subintervals with the proportional size of the intervals calculated in the beginning.\\
|
|
|
-To store as few informations as possible and due to the fact that fractions in binary have limited accuracity, only a single number, that lays between upper and lower end of the last intervall will be stored. To encode in binary, the binary floating point representation of any number inside the interval, for the last character is calculated, by using a similar process, described above.
|
|
|
+In the encoding process, the first symbol read from the sequence determines a interval, its symbol is associated with. Every following symbol determines a subinterval, which is determined by subdividing the previous interval into sections proportional to the probabilities from \ref{t:arith-prob}.
|
|
|
+Starting with \texttt{A}, the most left interval in \ref{k4:arith-unscaled} is subdivided into intervals visulaized below. Leaving a available space of $[0.0, 0.5)$. From there the interval, representing \texttt{G} is subdivided, and so on until the last symbol \texttt{C} is processed. This leaves a interval of $[0.40625, 0.421275)$.\\
|
|
|
+%To encode a text, subdividing is used, step by step on the text symbols from start to the end
|
|
|
+To store the encoding result in as few bits as possible, only a single number,between upper and lower end of the last intervall will be stored. To encode in binary, the binary floating point representation of any number inside the interval, for the last character is calculated.\\
|
|
|
+For this example, the number \texttt{0.41484375} in decimal, or \texttt{0.0110101} in binary, would be calculated.\\
|
|
|
+%todo compression ratio
|
|
|
To summarize the encoding process in short \cite{moffat_arith, witten87}:\\
|
|
|
|
|
|
\begin{itemize}
|
|
|
@@ -155,19 +192,16 @@ To summarize the encoding process in short \cite{moffat_arith, witten87}:\\
|
|
|
\item This process is repeated, until a interval for the last character is determined.
|
|
|
\item A binary floating point number is determined wich lays in between the interval that represents the represents the last symbol.\\
|
|
|
\end{itemize}
|
|
|
-% its finite subdividing because of the limitation that comes with processor architecture
|
|
|
|
|
|
+% its finite subdividing because of the limitation that comes with processor architecture
|
|
|
For the decoding process to work, the \ac{EOF} symbol must be be present as the last symbol in the text. The compressed file will store the probabilies of each alphabet symbol as well as the floatingpoint number. The decoding process executes in a simmilar procedure as the encoding. The stored probabilies determine intervals. Those will get subdivided, by using the encoded floating point as guidance, until the \ac{EOF} symbol is found. By noting in which interval the floating point is found, for every new subdivision, and projecting the probabilies associated with the intervals onto the alphabet, the origin text can be read \cite{witten87, moffat_arith, ris76}.\\
|
|
|
% rescaling
|
|
|
-% math and computers
|
|
|
-In computers, arithmetic operations on floating point numbers are processed with integer representations of given floating point number \cite{ieee-float}. The number 0.4 + would be represented by $4\cdot 10^-1$.\\
|
|
|
-Intervals for the first symbol would be represented by natural numbers between 0 and 100 and $... \cdot 10^-x$. \texttt{x} starts with the value 2 and grows as the intgers grow in length, meaning only if a uneven number is divided. For example: Dividing a uneven number like $5\cdot 10^-1$ by two, will result in $25\cdot 10^-2$. On the other hand, subdividing $4\cdot 10^y$ by two, with any negativ real number as y would not result in a greater \texttt{x} the length required to display the result will match the length required to display the input number \cite{witten87, moffat_arith}.\\
|
|
|
|
|
|
-% example
|
|
|
\begin{figure}[H]
|
|
|
\centering
|
|
|
- \includegraphics[width=15cm]{k4/arith-resize.png}
|
|
|
- \caption{Illustrative rescaling in arithmetic coding process. \cite{witten87}}
|
|
|
+ %\includegraphics[width=15cm]{k4/arith-resize.png}
|
|
|
+ \includegraphics[width=15cm]{k4/arith-scaled.png}
|
|
|
+ \caption{Illustrative rescaling in arithmetic coding process.}
|
|
|
\label{k4:rescale}
|
|
|
\end{figure}
|
|
|
|
|
|
@@ -214,10 +248,10 @@ The average length for any symbol encoded in \acs{ASCII} is eight, while only us
|
|
|
\toprule
|
|
|
\textbf{Symbol} & \textbf{\acs{ASCII} Code} & \textbf{Probability} & \textbf{Occurences}\\
|
|
|
\midrule
|
|
|
- A & 0100 0001 & $\frac{100}{11}=0.11$ & 11\\
|
|
|
- C & 0100 0011 & $\frac{100}{71}=0.71$ & 71\\
|
|
|
- G & 0101 0100 & $\frac{100}{13}=0.13$ & 13\\
|
|
|
- T & 0000 1010 & $\frac{100}{5}=0.05$ & 5\\
|
|
|
+ A & 0100 0001 & $\frac{11}{100}=0.11$ & 11\\
|
|
|
+ C & 0100 0011 & $\frac{71}{100}=0.71$ & 71\\
|
|
|
+ G & 0101 0100 & $\frac{13}{100}=0.13$ & 13\\
|
|
|
+ T & 0000 1010 & $\frac{5}{100}=0.05$ & 5\\
|
|
|
\bottomrule
|
|
|
\end{longtable}
|
|
|
\end{footnotesize}
|